Matrizes
Matrizes são objetos matemáticos organizados em linhas e colunas.
Cada um dos seus elementos tem dois índices (ai j). O primeiro índice i indica à linha e o segundo índice j a coluna. O número de linhas e colunas que uma matriz tem chama dimensão da matriz. A matriz ao lado tem m linhas e n colunas e dizemos que ela tem dimensão m x n (m por n) e a representamos por A = (ai j) m x n. Quando o número de linhas é igual ao número de colunas dizemos que a matriz é de ordem n e a chamamos de matriz quadrada.
Matrizes são objetos matemáticos organizados em linhas e colunas.
Cada um dos seus elementos tem dois índices (ai j). O primeiro índice i indica à linha e o segundo índice j a coluna. O número de linhas e colunas que uma matriz tem chama dimensão da matriz. A matriz ao lado tem m linhas e n colunas e dizemos que ela tem dimensão m x n (m por n) e a representamos por A = (ai j) m x n. Quando o número de linhas é igual ao número de colunas dizemos que a matriz é de ordem n e a chamamos de matriz quadrada.
Introdução
O crescente uso dos computadores tem feito com que a teoria das matrizes seja cada vez mais aplicada em áreas como Economia, Engenharia, Matemática, Física, dentre outras. Vejamos um exemplo.
A tabela a seguir representa as notas de três alunos em uma etapa:
Química
|
Inglês
|
Literatura
|
Espanhol
| |
A
|
8
|
7
|
9
|
8
|
B
|
6
|
6
|
7
|
6
|
C
|
4
|
8
|
5
|
9
|
Se quisermos saber a nota do aluno B em Literatura, basta procurar o número que fica na segunda linha e na terceira coluna da tabela.
Vamos agora considerar uma tabela de números dispostos em linhas e colunas, como no exemplo acima, mas colocados entre parênteses ou colchetes:
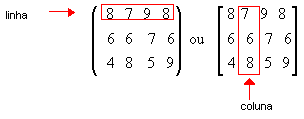
Em tabelas assim dispostas, os números são os elementos. As linhas são enumeradas de cima para baixo e as colunas, da esquerda para direita:
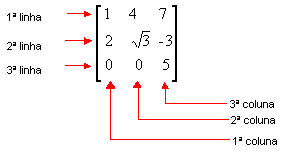
Tabelas com m linhas e n colunas ( m e n números naturais diferentes de 0) são denominadas matrizes m x n. Na tabela anterior temos, portanto, uma matriz 3 x 3.
Veja mais alguns exemplos:
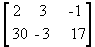 é uma matriz do tipo 2 x 3
é uma matriz do tipo 2 x 3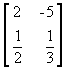 é uma matriz do tipo 2 x 2
é uma matriz do tipo 2 x 2
Notação geral
Costuma-se representar as matrizes por letras maiúsculas e seus elementos por letras minúsculas, acompanhadas por dois índices que indicam, respectivamente, a linha e a coluna que o elemento ocupa.
Assim, uma matriz A do tipo m x n é representada por:

ou, abreviadamente, A = [aij]m x n, em que i e j representam, respectivamente, a linha e a coluna que o elemento ocupa. Por exemplo, na matriz anterior, a23 é o elemento da 2ª linha e da 3ª coluna.
Na matriz 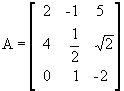 , temos:
, temos:
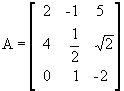 , temos:
, temos: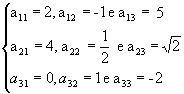
Ou na matriz B = [ -1 0 2 5 ], temos: a11 = -1, a12 = 0, a13 = 2 e a14 = 5.
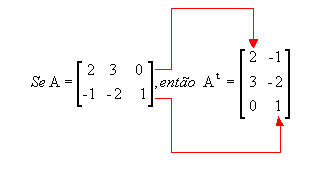
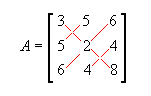 é simétrica, pois a12 = a21 = 5, a13 = a31 = 6, a23 = a32 = 4, ou seja, temos sempre a ij = a ij.
é simétrica, pois a12 = a21 = 5, a13 = a31 = 6, a23 = a32 = 4, ou seja, temos sempre a ij = a ij.
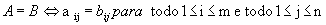
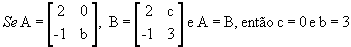 .
.
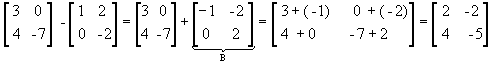
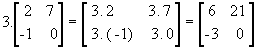
Denominações especiais
Algumas matrizes, por suas características, recebem denominações especiais.
- Matriz linha: matriz do tipo 1 x n, ou seja, com uma única linha. Por exemplo, a matriz A =[4 7 -3 1], do tipo 1 x 4.
- Matriz coluna: matriz do tipo m x 1, ou seja, com uma única coluna. Por exemplo,
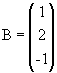 , do tipo 3 x 1
, do tipo 3 x 1
- Matriz quadrada: matriz do tipo n x n, ou seja, com o mesmo número de linhas e colunas; dizemos que a matriz é de ordem n. Por exemplo, a matriz
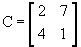 é do tipo 2 x 2, isto é, quadrada de ordem 2.
é do tipo 2 x 2, isto é, quadrada de ordem 2.
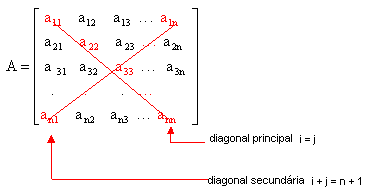
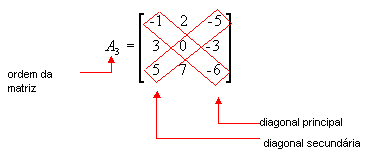
Numa matriz quadrada definimos a diagonal principal e a diagonal secundária. A principal é formada pelos elementos aij tais que i = j. Na secundária, temos i + j = n + 1.
Veja:

Observe a matriz a seguir:

a11 = -1 é elemento da diagonal principal, pis i = j = 1
a31= 5 é elemento da diagonal secundária, pois i + j = n + 1 ( 3 + 1 = 3 + 1)
- Matriz nula: matriz em que todos os elementos são nulos; é representada por 0m x n.
Por exemplo, 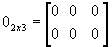 .
.
- Matriz diagonal: matriz quadrada em que todos os elementos que não estão na diagonal principal são nulos. Por exemplo:
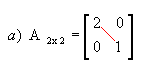 | 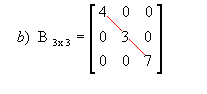 |
- Matriz identidade: matriz quadrada em que todos os elementos da diagonal principal são iguais a 1 e os demais são nulos; é representada por In, sendo n a ordem da matriz. Por exemplo:
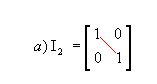 | 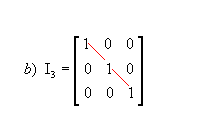 |
Assim, para uma matriz identidade 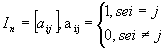 .
.
- Matriz transposta: matriz At obtida a partir da matriz A trocando-se ordenadamente as linhas por colunas ou as colunas por linhas. Por exemplo:
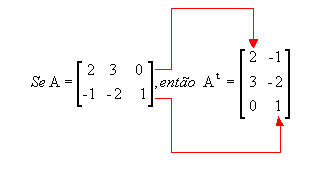
Desse modo, se a matriz A é do tipo m x n, At é do tipo n x m.
Note que a 1ª linha de A corresponde à 1ª coluna de At e a 2ª linha de A corresponde à 2ª coluna de At.
- Matriz simétrica: matriz quadrada de ordem n tal que A = At . Por exemplo,
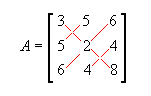 é simétrica, pois a12 = a21 = 5, a13 = a31 = 6, a23 = a32 = 4, ou seja, temos sempre a ij = a ij.
é simétrica, pois a12 = a21 = 5, a13 = a31 = 6, a23 = a32 = 4, ou seja, temos sempre a ij = a ij.- Matriz oposta: matriz -A obtida a partir de A trocando-se o sinal de todos os elementos de A. Por exemplo,
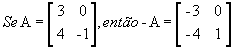 .
.
Igualdade de matrizes
Duas matrizes, A e B, do mesmo tipo m x n, são iguais se, e somente se, todos os elementos que ocupam a mesma posição são iguais:
Operações envolvendo matrizes
Adição
Dadas as matrizes 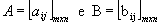 , chamamos de soma dessas matrizes a matriz
, chamamos de soma dessas matrizes a matriz 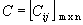 , tal que Cij = aij + bij , para todo
, tal que Cij = aij + bij , para todo 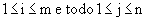 :
:
A + B = C
|
Exemplos:
Observação: A + B existe se, e somente se, A e B forem do mesmo tipo.
Propriedades
Sendo A, B e C matrizes do mesmo tipo ( m x n), temos as seguintes propriedades para a adição:
a) comutativa: A + B = B + A
b) associativa: ( A + B) + C = A + ( B + C)
c) elemento neutro: A + 0 = 0 + A = A, sendo 0 a matriz nula m x n
d) elemento oposto: A + ( - A) = (-A) + A = 0
Subtração
Dadas as matrizes 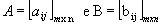 , chamamos de diferença entre essas matrizes a soma de A com a matriz oposta de B:
, chamamos de diferença entre essas matrizes a soma de A com a matriz oposta de B:
A - B = A + ( - B )
|
Observe:
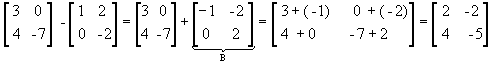
Multiplicação de um número real por uma matriz
Dados um número real x e uma matriz A do tipo m x n, o produto de x por A é uma matriz B do tipo m x n obtida pela multiplicação de cada elemento de A por x, ou seja, bij = xaij:
B = x.A
|
Observe o seguinte exemplo:
Propriedades
Sendo A e B matrizes do mesmo tipo ( m x n) e x e y números reais quaisquer, valem as seguintes propriedades:
a) associativa: x . (yA) = (xy) . A
b) distributiva de um número real em relação à adição de matrizes: x . (A + B) = xA + xB
c) distributiva de uma matriz em relação à adição de dois números reais: (x + y) . A = xA + yA
d) elemento neutro : xA = A, para x=1, ou seja, A=A
Matrizes
Multiplicação de matrizes
O produto de uma matriz por outra não é determinado por meio do produto dos sus respectivos elementos.
Assim, o produto das matrizes A = ( aij) m x p e B = ( bij) p x n é a matriz C = (cij) m x n em que cada elemento cij é obtido por meio da soma dos produtos dos elementos correspondentes da i-ésima linha de A pelos elementos da j-ésima coluna B.
Vamos multiplicar a matriz
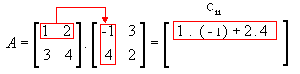
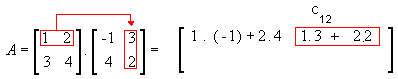
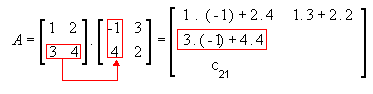
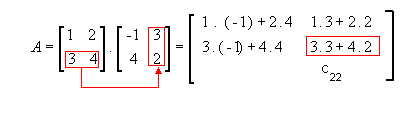
Assim,
Observe que:
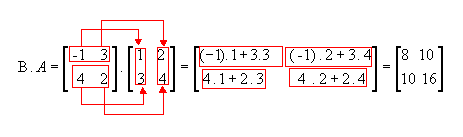
Portanto,
Vejamos outro exemplo com as matrizes
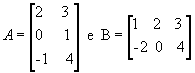 : :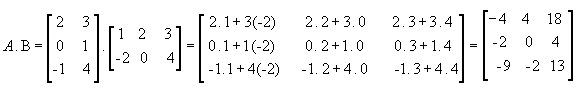 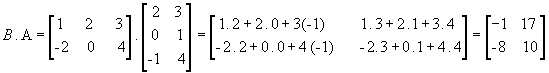
Da definição, temos que a matriz produto A . B só existe se o número de colunas de A for igual ao número de linhas de B:
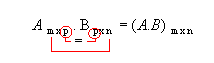
A matriz produto terá o número de linhas de A (m) e o número de colunas de B(n):
Propriedades
Verificadas as condições de existência para a multiplicação de matrizes, valem as seguintes propriedades:
a) associativa: ( A . B) . C = A . ( B . C )
b) distributiva em relação à adição: A . ( B + C ) = A . B + A . C ou ( A + B ) . C = A . C + B . C
c) elemento neutro: A . In = In . A = A, sendo In a matriz identidade de ordem n
Vimos que a propriedade comutativa, geralmente, não vale para a multiplicação de matrizes. Não vale também o anulamento do produto, ou seja: sendo 0 m x n uma matriz nula, A .B =0 m x n não implica, necessariamente, que A = 0 m x n ou B = 0 m x n.
Matriz inversa
Dada uma matriz A, quadrada, de ordem n, se existir uma matriz A', de mesma ordem, tal que A . A' = A' . A = In , então A' é matriz inversa de A . representamos a matriz inversa por A-1 .
Aplicações de matrizes
As matrizes são muito utilizadas na computação para representarmos translação, rotação, escala de objetos em computação gráfica, para se resolver sistemas de equações, etc.Na engenharia elétrica, é muito difícil resolver problemas de circuitos elétricos e linhas de transmissão de energia elétrica sem matrizes. Trabalhar com uma malha de linha de transmissão e passar esse circuito para forma matricial, mais fácil. Na mecânica também é muito importante, pois os tensores (grandeza) só são fornecidos em forma de matriz.Os determinantes simplificam e sistematizam a resolução de sistemas de equações lineares. Matriz quadrada é a que tem o mesmo número de linhas e de colunas (ou seja, é do tipo mxn). A toda matriz quadrada está associado um número ao qual damos o nome de determinante. Dentre as várias aplicações dos determinantes na Matemática, temos: -resolução de alguns tipos de sistemas de equações lineares; -cálculo da área de um triângulo situado no plano cartesiano, quando são conhecidas as coordenadas dos seus vértices. |
.jpg)
.jpg)
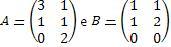




.png)

.png)
Amei...
ResponderExcluir